Đề thi tốt nghiệp môn Toán 2022

Đề thi và lời giải chi tiết đề thi tốt nghiệp môn Toán 2022 của bộ Giáo dục và Đào tạo!

Đề tham khảo tốt nghiệp môn Toán 2022

Đề thi và lời giải chi tiết để tham khảo tốt nghiệp môn Toán 2022 của bộ Giáo dục và Đào tạo!

Giải chi tiết đề thi Tốt nghiệp THPT 2021, môn Toán, mã đề 101 và 105

Lời giải chi tiết đề thi Tốt nghiệp THPT 2021, môn Toán, khóa ngày 7/7/2021.

Mã đề 101

Click to access 2021made101-2.pdf

Mã đề 105

Click to access 2021made105-1.pdf

Phân loại câu hỏi trong các đề thi THPTQG của Bộ GD và ĐT (lời giải)

Tài liệu tổng hợp các đề thi (tham khảo và chính thức) của bộ GD và ĐT từ năm 2017 đến năm 2020. Các câu hỏi đều được phân dạng và sắp xếp từ dễ đến khó. Tài liệu bao gồm các câu hỏi với đáp án và lời giải chi tiết nhằm giúp học sinh tham khảo sau khi đã tự mình làm bài tập.

Click to access plchthptqg2017-2020-loigiai.pdf

Phân loại câu hỏi trong các đề thi THPTQG của Bộ GD và ĐT

Tài liệu tổng hợp các đề thi (tham khảo và chính thức) của bộ GD và ĐT từ năm 2017 đến năm 2020. Các câu hỏi đều được phân dạng và sắp xếp từ dễ đến khó. Tài liệu chỉ bao gồm các câu hỏi không có đáp án và lời giải nhằm giúp học sinh tự mình khám phá lời giải của riêng mình!

Click to access plchthptqg2017-2020-de.pdf

Giải chi tiết đề thi THPT Quốc Gia 2018, mã đề 101 môn Toán

Câu 36
Có bao nhiêu giá trị nguyên của tham số $m$ để hàm số $y=x^8+(m-2)x^5-(m^2-4)x^4+1$ đạt cực tiểu tại $x=0$ ?
A. $3$ .
B. $5$ .
C. $4$ .
D. Vô số.

Lời giải

Chọn phương án C.

Ta có $y'=8x^7+5(m-2)x^4-4(m^2-4)x^3=x^3\left( 8x^4+5(m-2)x-4(m^2-4) \right)$ .

Đặt $f(x)=8x^4+5(m-2)x-4(m^2-4)$ , ta xét hai trường hợp:

• TH1: $f(0)=0\Leftrightarrow m^2-4=0\Leftrightarrow m=\pm 2$ .

Với $m=2\Rightarrow y'=8x^7\Rightarrow x=0$ là điểm cực tiểu.

Với $m=-2\Rightarrow y'=x^4\left( 8x^4-20\right) \Rightarrow x=0$ không phải là điểm cực tiểu.

• TH2: $f(0)\neq 0\Leftrightarrow m^2-4\neq 0\Leftrightarrow m\neq \pm 2$ .

Hàm số đạt cực tiểu tại $x=0$ khi và chỉ khi $y'=x^3.f(x)$ đổi dấu từ $-$ qua $+$ khi qua $x=0$ .

Điều này tương đương với $\lim\limits_{x\to 0}f(x)>0\Leftrightarrow m^2-4<0\Leftrightarrow -2<m<2$ .

Kết hợp ta có bốn giá trị nguyên của $m$ thỏa mãn yêu cầu bài toán.

Câu 37
Cho hình lập phương $ABCD. A'B'C'D'$ có tâm $O$ . Gọi $I$ là tâm hình vuông $A'B'C'D'$ và $M$ là điểm thuộc đoạn thẳng $OI$ sao cho $MO=2MI$ (tham khảo hình vẽ). Khi đó côsin của góc tạo bởi hai mặt phẳng $(MC'D')$ và $(MAB)$ bằng

Hinh37a

A. $\dfrac{6\sqrt{85}}{85}$ .
B. $\dfrac{7\sqrt{85}}{85}$ .
C. $\dfrac{17\sqrt{13}}{65}$ .
D. $\dfrac{6\sqrt{13}}{65}$ .

Lời giải
Chọn phương án B.

Hinh37b

Gọi $P,Q$ lần lượt là trung điểm của $D'C'$ và $AB$ .

Ta có $\begin{cases} MP\perp C'D' \parallel AB\\ MQ\perp AB \end{cases}\Rightarrow AB\perp (MPQ)$ .

Suy ra $(MAB)\perp (MPQ)$ và $(MC'D')\perp (MPQ)$ .

Do đó góc giữa $(MAB)$ và $(MC'D')$ bằng góc giữa $MQ$ và $MP$ .

Đặt $AB=a$ , ta có $OI=\dfrac{a}{2}\Rightarrow MI=\dfrac{1}{3}OI=\dfrac{a}{6}$ .

Gọi $K$ là tâm của $ABCD$ , ta có $MK=IK-MI=\dfrac{5a}{6}$ .

Suy ra $MP=\sqrt{MI^2+IP^2}=\dfrac{\sqrt{10}a}{6}, MQ=\sqrt{MK^2+KQ^2}=\dfrac{\sqrt{34}a}{6}, PQ=\sqrt{2}a$ .

Vậy $\cos\alpha=|\cos \widehat{PMQ}|=\dfrac{\left|MP^2+MQ^2-PQ^2\right|}{2MP.MQ}=\dfrac{7\sqrt{85}}{85}$ .

Câu 42
Cho khối lăng trụ $ABC. A'B'C'$ , khoảng cách từ $C$ đến đường thẳng $BB'$ bằng $2$ , khoảng cách từ $A$ đến các đường thẳng $BB'$ và $CC'$ lần lượt bằng $1$ và $\sqrt{3}$ , hình chiếu vuông góc của $A$ lên mặt phẳng $\left(A'B'C'\right)$ là trung điểm $M$ của $B'C'$ và $A'M=\dfrac{2\sqrt{3}}{3}$ . Thể tích của khối lăng trụ đã cho bằng
A. $2$ .
B. $1$ .
C. $\sqrt{3}$ .
D. $\dfrac{2\sqrt{3}}{3}$ .

Lời giải

Chọn phương án A.

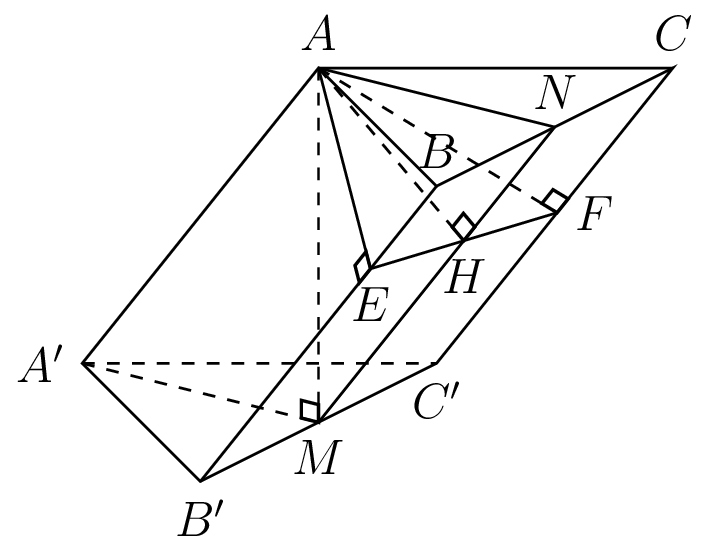
Hinh42b

Gọi $E$ , $F$ là hình chiếu của $A$ trên $BB'$ và $CC'$ .

Ta có $\begin{cases} AE\perp AA'\\ AF\perp AA' \end{cases}\Rightarrow AA'\perp (AEF)\Rightarrow BB'\perp EF$ .

Từ đó suy ra $EF=d(F,BB')=d(C,BB')=2\Rightarrow \triangle AEF$ vuông tại $A$ .

Gọi $N$ trung điểm $BC$ và $H=MN\cap EF$ , ta có $AH=\dfrac{1}{2}EF=1$ .

Dễ thấy $\triangle AMN$ vuông tại $A$ và có đường cao $AH$ .

Do đó $\dfrac{1}{AM^2}=\dfrac{1}{AH^2}-\dfrac{1}{AN^2}=\dfrac{1}{4}\Rightarrow AM=2$ .

Lại có $MN=\sqrt{AM^2+AN^2}=\dfrac{4}{\sqrt{3}}\Rightarrow S_{BCC'B'}=MN.EF=\dfrac{8}{\sqrt{3}}$ .

Vậy $V_{ABC.A'B'C'}=3V_{ABCC'}=\dfrac{3}{2}V_{A.BCC'B'}=\dfrac{1}{2}S_{BCC'B'}.\mathrm{d}(A,EF)=\dfrac{1}{2}.\dfrac{8}{\sqrt{3}}.\dfrac{\sqrt{3}}{2}=2$ .

Câu 43
Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên thuộc đoạn $[1;17]$ . Xác suất để ba số được viết ra có tổng chia hết cho $3$ bằng
A. $\dfrac{1728}{4913}$ .
B. $\dfrac{1079}{4913}$ .
C. $\dfrac{23}{68}$ .
D. $\dfrac{1637}{4913}$ .

Lời giải

Chọn phương án D.

Mỗi bạn có $17$ khả năng viết số nên số phần tử không gian mẫu là $17^3=4913$ .

Ta chia các số tự nhiên từ $1$ đến $17$ thành $3$ nhóm: Nhóm I gồm các số chia hết cho $3$ có $5$ số; nhóm II gồm các số chia cho $3$ dư $1$ gồm $6$ số; nhóm III gồm các số chia cho $3$ dư $2$ có $6$ số.

Ba bạn A, B, C mỗi bạn viết ngẫu nhiên lên bảng một số tự nhiên có tổng chia hết cho $3$ gồm các trường hợp sau:

• TH1: Ba số đều chia hết cho $3$ có $5^3=125$ cách.

• TH2: Ba số đều chia cho $3$ dư $1$ có $6^3=216$ cách.

• TH3: Ba số đều chia cho $3$ dư $2$ có $6^3=216$ cách.

• TH4: Một số chia hết cho $3$ , một số chia cho $3$ dư $1$ và một số chia cho $3$ dư $2$ có $5.6.6.3!=1080$ cách.

Từ đó suy ra số cách viết thỏa mãn yêu cầu bài toán là $125+216+216+1080=1637$ .

Vậy xác suất cần tìm là $\dfrac{1637}{4913}$ .

Câu 50

Cho hai hàm số $y=f(x)$ , $y=g(x)$ . Hai hàm số $y=f'(x)$ và $y=g'(x)$ có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số $y=g'(x)$ . Hàm số $h(x)=f(x+4)-g\left(2x-\dfrac{3}{2}\right)$ đồng biến trên khoảng nào dưới đây?

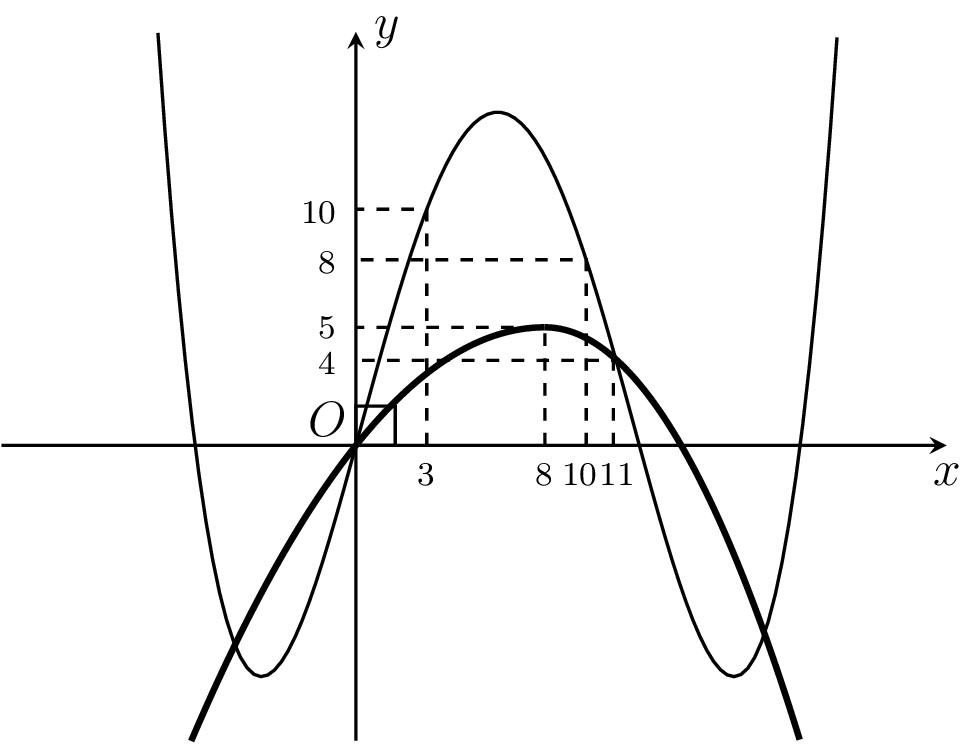
Hinh50a
A. $\left(5;\dfrac{31}{5}\right)$ .
B. $\left(\dfrac{9}{4};3\right)$ .
C. $\left(\dfrac{31}{5};+\infty \right)$ .
D. $\left(6;\dfrac{25}{4}\right)$ .

Lời giải

Chọn phương án B.

Ta có $h'(x)=f'(x+4)-2g'\left(2x-\dfrac{3}{2}\right)$ .

Xét $x=6,1$ , ta có $h'(6,1)=f'(10,1)-2g'(10,7)$ ; từ đồ thị ta có $f'(10,1)<f'(10)=8$ và $2g'(10,7)>2g'(11)=8\Rightarrow h'(6,1)<0$ nên loại phương án A và D.

Xét $x=6,25$ , ta có $h'(6,25)=f'(10,25)-2g'(11)$ ; từ đồ thị ta có $f'(10,25)<f'(10)=8$ và $2g'(1)=8\Rightarrow h'(6,25)<0$ nên loại phương án C.

Tải về đề thi theo liên kết sau: 2018.Made101;
Tải về hướng dẫn giải chi tiết đầy đủ theo liên kết sau: 2018.Made101.DA.

Định lý Ceva và ứng dụng

Định lý Ceva là một định lý phổ biến trong hình học dùng để chứng minh ba đường thẳng đồng quy.

A. Kiến Thức Cần Nhớ

1. Phép thử ngẫu nhiên.

• Phép thử ngẫu nhiên là một thí nghiệm hay một hành động mà :

-Kết quả của nó không dự đoán trước được;

-Có thể xác định được tập hợp tất cả các kết quả có thể xảy ra của phép thử đó.

• Tập tất cả các kết quả có thể xảy ra của phép thử gọi là không gian mẫu của phép thử, ký hiệu $\Omega$ .

2. Biến cố.

• Một biến cố $A$ liên quan tới phép thử $T$ được mô tả bởi một tập con ${\Omega _A}$ của không gian mẫu. Biến cố $A$ xảy ra khi kết quả của $T$ thuộc $\Omega_A$ . Mỗi phần tử của $\Omega_A$ gọi là một kết quả thuận lợi cho $A$ .

• Biến cố hợp : Là biến cố “ $A$ hoặc $B$ xảy ra”, ký hiệu $A\cup B$ . Ta có $\Omega_{A\cup B}=\Omega_A\cup \Omega_B$ .

• Biến cố giao : Là biến cố “Cả $A$ và $B$ cùng xảy ra”, ký hiệu $A\cap B$ . Ta có $\Omega_{A\cap B}=\Omega_A\cap \Omega_B$ .

• Biến cố đối : Là biến cố “Không xảy ra $A$ “, ký hiệu $\overline{A}$ . Ta có $\left( {{\Omega _{\overline A }} = \Omega \backslash {\Omega _A}} \right)$ .

• Biến cố xung khắc : Là hai biến cố $A$ và $B$ mà nếu $A$ xảy ra thì $B$ không xảy ra và ngược lại.

• Biến cố độc lập : Là hai biến cố $A$ và $B$ mà việc xảy ra hay không xảy ra $A$ không ảnh hưởng đến việc xảy ra hay không xảy ra $B$ và ngược lại.

3. Xác suất của một biến cố.

• Giả sử phép thử $T$ có không gian mẫu $\Omega$ là một tập hữu hạn và các kết quả của $T$ là đồng khả năng. Nếu $A$ là một biến cố liên quan đến phép thử $T$ thì xác suất của $A$ là một số, ký hiệu là $P(A)$ , được xác định bởi công thức $P(A)=\dfrac{\left|\Omega_A\right|}{|\Omega|}$ .

Sucsac

• Tính chất : $0 \leqslant P\left( A \right) \leqslant 1$ , $P\left( \emptyset \right) = 0$ , $P\left( \Omega \right) = 1$ , $P\left( {\overline A } \right) = 1 - P\left( A \right)$ .

• Quy tắc cộng xác suất : Nếu $A,B$ xung khắc thì $P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)$ .

• Quy tắc nhân xác suất : Nếu $A,B$ độc lập thì $P\left( {A \cap B} \right) = P\left( {AB} \right) = P\left( A \right)\times P\left( B \right)$ .

4. Biến ngẫu nhiên rời rạc.

• Là giá trị độc lập $X = \left\{ {{x_1},{x_2},...,{x_n}} \right\}$ nhận kết quả bằng số, hữu hạn và không dự đoán trước được.

• Xác suất tại ${x_k}$ : $P\left( {X = {x_k}} \right) = {p_k},\left( {k = 1..n} \right)$ . Khi đó ${p_1} + {p_2} + ... + {p_n} = 1$ .

• Bảng phân bố xác suất : $\begin{array}{|c|c c c|c c c|c c c|c c c|} \hline X& &x_1& & &x_2& & &...& & &x_n& \\ \hline P& &p_1& & &p_2& & &...& & &p_n& \\ \hline \end{array}$

• Kỳ vọng : $E\left( X \right) = \sum\limits_{i = 1}^n {{x_i}{p_i}}$ .

• Phương sai : $V\left( X \right) = \sum\limits_{i = 1}^n {x_i^2{p_i} - {E^2}\left( X \right)}$ .

• Độ lệch chuẩn : $\sigma \left( X \right) = \sqrt {V\left( X \right)}$ .
» xem tiếp

Giải chi tiết đề thi THPT Quốc Gia 2017, mã đề 101 môn Toán

TẢI VỀ HƯỚNG DẪN GIẢI

TẢI VỀ ĐỀ THI VÀ ĐÁP ÁN

Tuyển tập các đề thi thử THPT Quốc Gia trên báo Toán học & Tuổi Trẻ

Tài liệu gồm tuyển tập các đề thi thử THPT Quốc Gia trên báo Toán học & Tuổi Trẻ cùng với đáp án và lời giải chi tiết.
Xem và tải về tài liệu theo liên kết sau : De Thi Thu THTT

Đề Thi Thử THPTQG Của Trường THPT Phan Đình Phùng

Trích MÃ ĐỀ 101

Câu 1. Đồ thị hàm số $y=\dfrac{2x+3}{1-x}$ có phương trình đường tiệm cận ngang là
A. $y=2$
B. $y=1$
C. $y=-2$
D. $x=-2$

Câu 2. Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây ?
preview
A. $y=x^2-3x+4$
B. $y=x^4-2x^2+4$
C. $y=-x^3+3x^2+4$
D. $y=x^3-3x^2+4$

Câu 3. Hàm số $y=-x^3+3x-2$ nghịch biến trên các khoảng nào dưới đây ?
A. $(-\infty;-1)$ và $(1;+\infty)$
B. $(-\infty;0)$ và $(1;+\infty)$
C. $(-1;1)$
D. $(0;1)$

Câu 4. Số điểm cực trị của hàm số $y=-x^4+4x^2+1$ là
A. $2$
B. $3$
C. $0$
D. $1$

Câu 5. Giá trị cực tiểu của hàm số $y=-2x^3-3x^2+1$ là
A. $0$
B. $1$
C. $-1$
D. $-4$

Câu 6. Giá trị nhỏ nhất của hàm số $y=x^4+2x^2$ trên đoạn $[-2;-1]$ là
A. $0$
B. $24$
C. $3$
D. $-2$

Câu 7. Bảng biến thiên trong hình bên là bảng biến thiên của hàm số nào trong bốn hàm số dưới đây ?
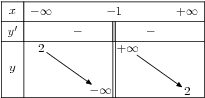
preview (2)
A. $y=\dfrac{-2x+1}{x+1}$
B. $y=\dfrac{2x+3}{x+1}$
C. $y=\dfrac{2x+3}{x-1}$
D. $y=\dfrac{2x+1}{x+1}$

Câu 8. Khoảng cách giữa hai điểm cực trị của đồ thị hàm số $y=x^3+3x^2$ là
A. $4$
B. $2$
C. $5\sqrt 2$
D. $2\sqrt{5}$

Câu 9. Giá trị của $m$ để đồ thị hàm số $y=x^3-3x^2+(m-1)x+1$ cắt đường thẳng $y=1$ tại ba điểm phân biệt là
A. $m\dfrac{13}{4}$ và $m\ne 1$
B. $m>\dfrac{13}{4}$
C. $m<\dfrac{13}{4}$
D. $m\leqslant \dfrac{13}{4}$

Câu 10. Giá trị của $m$ để hàm số $y=-x^3+mx^2-m$ đồng biến trên khoảng $(1;2)$ là
A. $m\in [2;3]$
B. $m\in [3;+\infty)$
C. $m\in \mathbb{R}$
D. $m\in [2;+\infty)$

Câu 11. Cho $R$ là một số thực dương và hình chữ nhật $MNPQ$ nội tiếp trong một nửa đường tròn đường kính $AB=2R$ , trong đó $MN$ nằm trên $AB$ . Tính tỉ số $k=\dfrac{MN}{MQ}$ để chu vi hình chữ nhật là lớn nhất.
preview (1)
A. $k=3$
B. $k=1$
C. $k=2$
D. $k=4$